https://arxiv.org/abs/1512.03385

Backgrounds

Batch Normalization

https://arxiv.org/abs/1502.03167

Batch Normalization(이하 BN) 은 활성함수에 입력되기 직전의 선형 출력을 미니배치 단위로 평균 0, 분산 1로 정규화 하는 기법이며, 기울기 소실/폭발 현상을 완화할 수 있는 방법이다.

레이어의 forward 연산은 $z=Wx, \quad a=f(z)$ 이고 (바이어스 생략), 역전파는:

$$\frac{dL}{dx}=W^T(\frac{dL}{da}\odot f'(z))$$

이다.

$f'$ 는 활성함수의 도함수이므로:

$$\text{sigmoid}'(z)\in(0, 1) \quad \tanh'(z)\in(0, 1) \quad \text{ReLU}'(z)\in\{0, 1\}$$

이다. 즉 활성함수의 도함수는 기울기를 증폭시키지 못하므로, 역전파에서 기울기 폭발의 주요 원인은 가중치 행렬 $W^T$ 의 스케일이다.

또, $W$ 의 스케일이 큰 경우, 작은 $x$ 의 변화에도 $z$ 의 값이 크게 변화하게 된다. 즉 $z$ 의 분산이 커지며, $z$ 분포의 상당 부분이 활성함수의 포화 영역에 위치하게 된다.

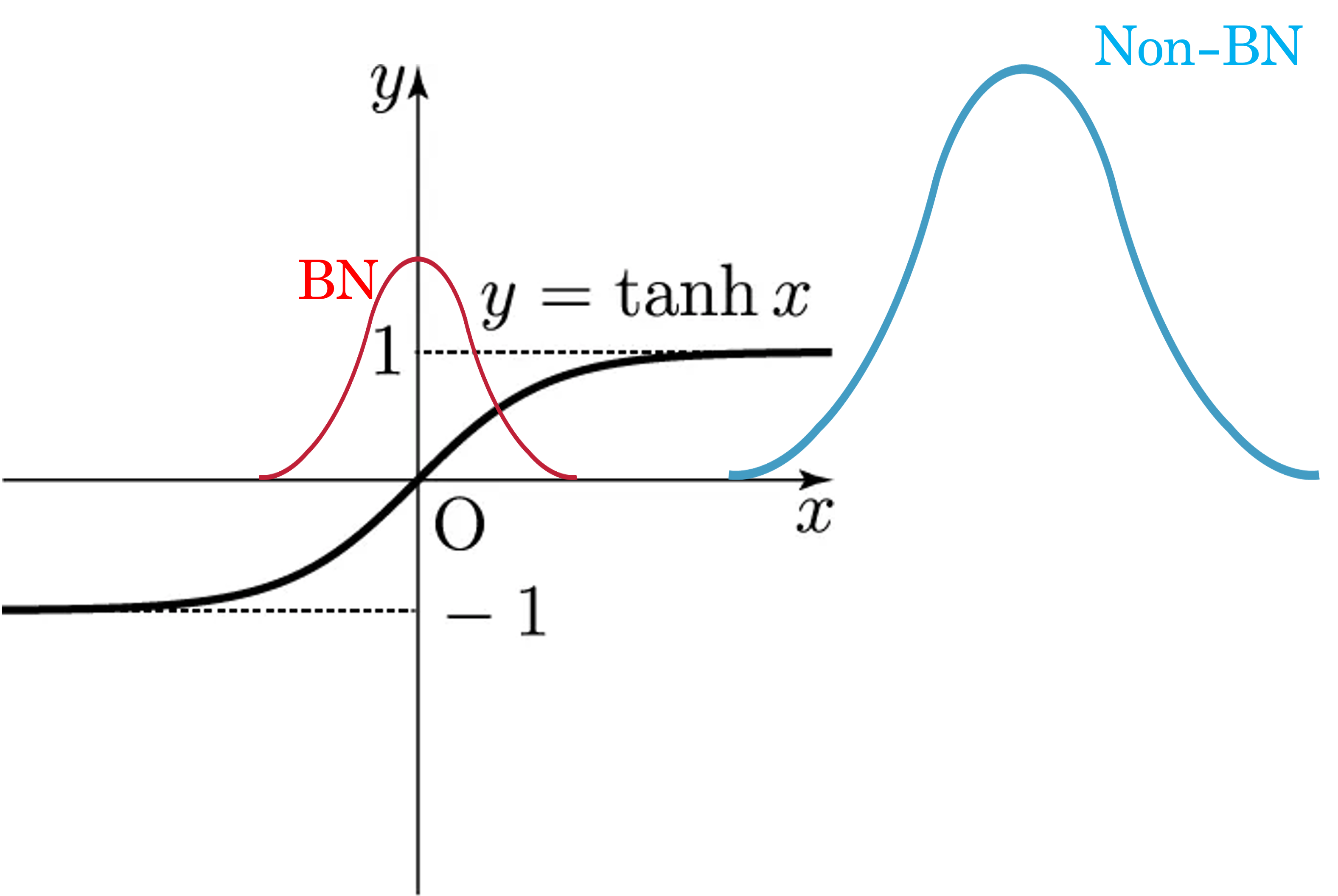
사진처럼 활성함수가 $\text{tanh}$ 인 경우, $z$ 의 분포가 1 이상일 때 $f'(z)$ 는 극단적으로 작아지게 된다. 곧 역전파에서 $\frac{dL}{da}\odot f'(z)$ 의 값이 작아지므로, 기울기가 소실된다.

그래서 BN 은 $z$ 가 활성함수로 들어가기 전에 미니배치($_B$) 단위로 정규화 하여 활성함수의 중앙 부분에 $z$ 가 분포하도록 강제한다.

$$\hat{z} = \frac{z - \mu_B}{\sqrt{\sigma^2_B+\epsilon}} \quad y=\gamma\hat{z}+\beta$$

단순히 스케일을 정규화하는 것이 아니라, 학습 파라미터 $\gamma, \beta$ 를 사용하여 입력 분포를 스케일 하거나 이동시킬 수 있게 한다. 즉 $\gamma, \beta$ 는 정규화로 사라진 스케일과 자유도를 복원하여 네트워크가 필요한 경우 선형 변환을 다시 학습할 수 있도록 한다.

VGG

https://arxiv.org/abs/1409.1556

VGG는 작은 3×3 convolution을 반복적으로 쌓아 깊이를 늘리면 성능이 좋아진다는 것을 처음으로 명확히 보여준 CNN이다. 공간 해상도는 pooling으로 줄이고 채널 수를 늘리며, 저수준 특징에서 고수준 개념으로 가는 계층적 표현을 형성한다는 점에서 다양한 CNN 설계의 레퍼런스가 되었다.

반면 한계도 분명하다. fully connected 레이어로 인해 파라미터 수와 연산량이 과도하게 크고, BN이나 residual connection이 없어 더 깊은 구조로 확장하기 어렵다. 또한 pooling 중심의 downsampling은 위치 정보 손실을 초래한다.

Faster R-CNN

https://arxiv.org/abs/1506.01497

R-CNN은 객체 검출을 “영역 제안 + CNN 분류”로 분해한 최초의 실용적 방법이다. 먼저 Selective Search로 이미지당 약 2천 개의 region proposal을 만들고, 각 영역을 개별적으로 CNN에 통과시켜 feature를 뽑은 뒤 분류하고 bounding box regression으로 위치를 보정한다.

이 방식은 CNN의 강력한 표현력을 detection에 처음 성공적으로 도입했다는 점에서 의미가 크지만, 모든 proposal을 독립적으로 CNN에 넣는 구조 때문에 계산량과 저장 비용이 비현실적으로 크고, 학습 파이프라인도 여러 단계로 분리돼 있다.

Faster R-CNN은 R-CNN 계열의 병목이던 region proposal 자체를 신경망 안으로 흡수했다. Selective Search를 제거하고, convolution feature map 위에서 RPN(Region Proposal Network)이 proposal을 생성한다. 이 proposal들은 RoI(Region of Interest) Pooling을 통해 고정 크기 feature로 변환되어, 하나의 CNN backbone을 proposal 생성과 분류가 공유한다.

결과적으로 Faster R-CNN은 정확도를 유지하면서도 속도를 획기적으로 개선했다.

Introduction

깊은 합성공 신경망(CNN) 은 이미지 분류 분야에서 엄청난 돌파구를 만들어냈다. 전통적인 이미지 인색 파이프라인은 가장자리, 곡선 등을 검출하는 Low-level 단계, part, pattern 을 검출하는 Mid-level, 얼굴, 사물 등을 인식하는 High-level, 그리고 classifier 까지, 명시적으로 구분된 단계가 있었으며 이를 사람이 단계별로 설계했고, 각 단계는 따로 최적화 되었다.

CNN 은 Image 로 부터 classifier 까지 전 과정을 하나의 네트워크가 알아서 학습하도록 하며, 계층적 표현 + 분류기가 하나의 깊은 함수로 묶여 있어 end-to-end 모델을 구성할 수 있었다.

CNN 에서 이러한 특징의 Level 은 레이어를 더 깊이 쌓을 수록 더욱 풍부해질 수 있다. 이는 네트워크의 깊이가 늘어날 수록 표현력이 증가함을 의미하고, 관련 연구들이 네트워크의 깊이가 결정적으로 중요하다는 것을 보여준다. 난이도가 높은 ImageNet 데이터셋에서 최고 성능을 낸 모델들은 모두 매우 깊은 모델을 사용한다. (VGG-16, VGG-19, GoogLeNet 등)

detection, segmentation, pose estimation 같은 고난도의 시각 인식 문제들에서도 깊은 모델은 효과가 있었다. 이는 깊은 네트워크가 classification 뿐만 아니라 범용적인 이점으로 작용함을 의미한다.

이처럼 깊은 네트워크의 중요성이 커지면서 의문이 생긴다.

단순히 레이어만 더 쌓는 것만으로 더 좋은 네트워크를 학습할 수 있는가?

이 질문에 대한 답은 gradient vanishing/exploding 에 의해 가로막힌다. 이 문제는 학습 초반부터 모델 최적화를 방해한다. 이 문제는 normalized initialization, batch normalization 에 의해 상당 부분 해결되었고, 이로 인해 깊은 네트워크에서도 SGD + 역전파로 학습을 시작할 수 있게 되었다.

그러나 학습을 시작할 수 있는 것과 얼마나 최적화할 수 있는지는 별개의 문제이다. 저자는 실험 결과를 통해 깊은 네트워크에서 얇은 네트워크보다 training/test error 가 높게 나타나는 현상(degradation)에 주목한다.

degradation은 적절히 깊은 모델에 더 많은 레이어를 추가했을 때 관측되며, 이는 training accuracy 자체가 떨어지기 때문에 과적합에 의한 문제가 아니다.

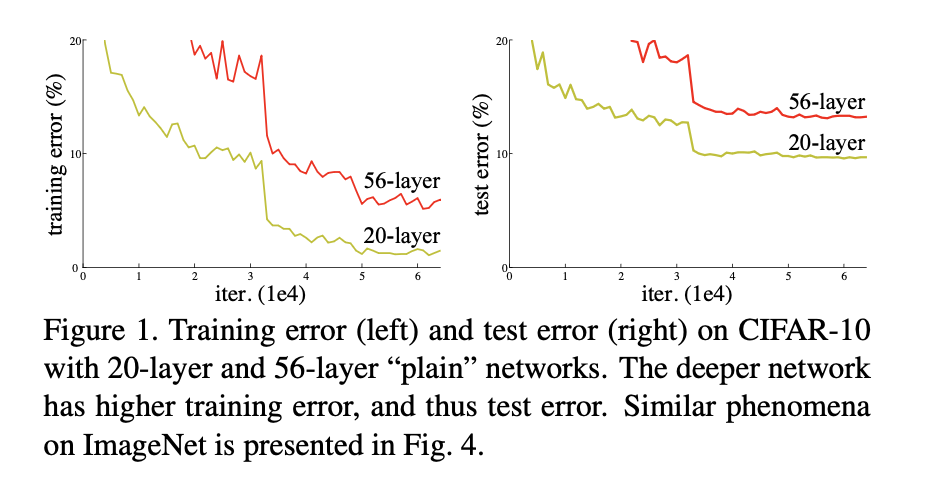
이는 표현력 관점에서 말이 되지 않는다. 만약 적당한 깊이의 네트워크가 있을 때, 여기서 레이어를 더 추가한 깊은 네트워크를 생각해보자.

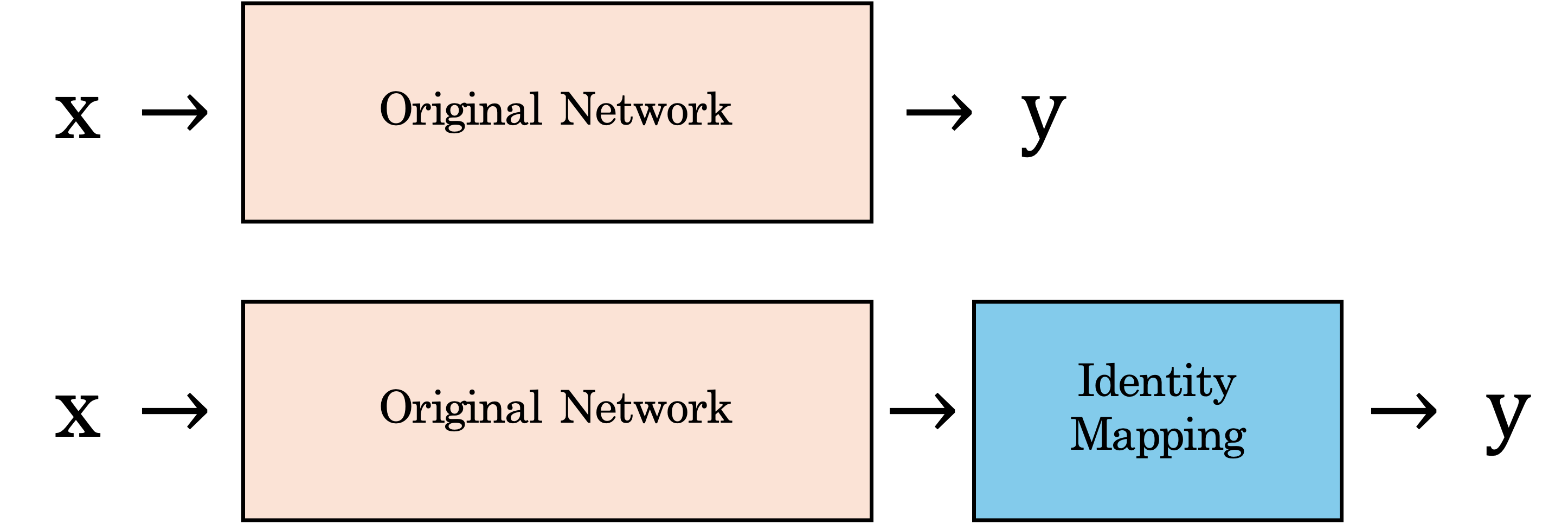
더 깊은 네트워크를 만들기 위해 기존 네트워크 위에 새로운 레이어들을 추가하고, 기존 Original Network의 가중치와 바이어스를 그대로 복사한다고 가정하자.

이때 새로 추가된 레이어들이 모두 항등함수(identity mapping)를 구현한다면, 확장된 깊은 네트워크는 깊어지기 전의 Original Network와 동일한 training/test error를 갖는 해(solution)를 표현할 수 있다.

즉, 더 깊은 네트워크는 얕은 네트워크를 포함하는 함수 공간을 가지며, 추가된 레이어가 항등함수를 구현할 수 있다면 얕은 네트워크에서 얻어진 해는 깊은 네트워크에서도 그대로 재현 가능하다. 따라서 깊은 네트워크의 최소 training error는 얕은 네트워크보다 클 수 없다.

그럼에도 불구하고 실제 학습 과정에서 SGD가 이러한 해를 찾지 못한다는 사실은 관측되는 degradation 현상이 overfitting과 무관하며, 모델 구조 자체가 최적화 관점에서 어려움을 가지고 있음을 시사한다.

이에 저자는 identity mapping 을 모델이 구조적으로 쉽게 표현할 수 있도록 residual function을 도입한 ResNet 구조를 제안한다. 이는 단순히 더 깊은 네트워크를 가능하게 한 것이 아니라, 존재하지만 SGD가 찾기 어려웠던 해를 구조적으로 쉽게 최적화할 수 있도록 만든 설계이다.

Residual Block

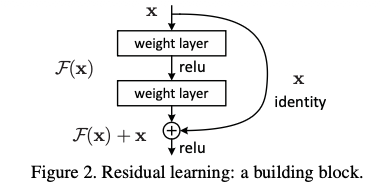
저자는 degradation 문제를 해결하기 위해 여러 개의 레이어를 단순히 쌓아서 원하는 함수를 직접 근사하길 기대하는 대신, 레이어들이 Residual 함수를 학습하도록 명시적으로 설계한다.

학습되길 원하는 목표 함수를 $H(x)$ 라고 할 때, 비선형 레이어들이

$$F(x) := H(x) - x$$

라는 또 다른 함수를 학습하도록 한다.

즉 네트워크가 직접 $H(x)$ 를 학습하는 것이 아니라, 입력 $x$ 에서 얼마나 변화해야 하는지, 즉 변화량을 의미하는 $F(x)$ 만을 학습하게 하는 것이다. 이를 이항하면 목표 함수는

$$H(x) = F(x) + x$$

로 다시 표현된다.

저자는 참조 없이 처음부터 학습해야 하는 기존의 $H(x)$ 보다, Residual 함수 $F(x)$ 를 최적화하는 것이 더 쉽다고 주장한다. 특히 최적의 $H(x)$ 가 항등 함수인 경우, 여러 비선형 레이어를 통해 $H(x)=x$ 를 학습하는 것보다 $F(x)=0$ 을 만드는 것이 훨씬 쉽기 때문이다.

즉, Plain Network에서는 모델이 항등함수를 스스로 만들어야 하므로 최적화가 어렵지만, ResNet에서는 $F(x)$ 가 0이 되기만 하면 되므로 최적화가 훨씬 수월해진다는 것이 핵심 주장이다.

저자는 Residual block이

$$y = F(x) + x$$

형태를 가질 때, 입력 $x$ 가 조금 변하더라도 출력은 항상 입력 변화가 그대로 전달되는 경로를 포함하게 되므로 여러 residual block을 깊게 쌓더라도 기울기가 레이어를 지나며 급격히 줄어들거나 커지지 않고 안정적으로 전달되며 결과적으로 깊은 네트워크에서도 기울기 소실이나 폭발을 완화할 수 있다고 주장한다.

이러한 $F(x)+x$ 구조는 shortcut connection을 가진 forward 신경망으로 구현할 수 있으며, 곱셈이 아닌 덧셈 연산만을 사용하므로 추가적인 파라미터나 계산 복잡도를 요구하지 않는다. 전체 네트워크는 기존과 동일하게 SGD와 역전파를 통해 end-to-end로 학습할 수 있다.

저자는 CIFAR-10 데이터셋에서도 plain network에서 degradation 현상이 관측됨을 보이고, 이를 residual network로 해결함으로써 제안한 방법이 특정 데이터셋에 국한된 현상이 아니라 깊은 네트워크의 최적화 문제 전반에 적용 가능한 일반적인 방법임을 주장한다.

또한 기존 네트워크보다 훨씬 더 깊은 구조에서도 모델을 안정적으로 학습시켰으며, 1000개 이상의 레이어를 가진 네트워크까지 탐구함으로써 제안한 구조가 깊이에 따른 최적화 한계를 실질적으로 극복함을 보였다.

Related Works

Residual Representations

VLAD

이미지 분류/검색 문제에서는 이미지의 수천개의 로컬 특징들을 하나의 고정길이 벡터로 요약하여야 하는데, 고전적인 BoVW 기법에서는 “어떤 패턴이 몇번 나왔나” 만 카운팅한다. 곧 평균적인 정보만 남고 세부 구조는 소실되는데, VLAD는 각 로컬 특징 $x$ 에 대해 가장 가까운 대표 벡터 $c$ 를 찾아 residual $(x - c)$ 을 누적한다. 즉 특징 자체가 아니라 기준점에서의 잔차를 표현으로 사용한다.

residual 은 평균이 0 근처이며 분포가 단순하여 shallow 구조에서도 높은 성능을 냈다. 즉 VLAD 는 네트워크가 깊지 않아도 residual 표현 만으로 높은 성능을 기록했으며, 이는 residual learning 으로 문제를 해결한 연구 중 하나이다.

Multigrid

편미분방정식을 직접 풀면 변수가 많고 수렴이 매우 느리다. multigrid 는 해를 한번에 정확하게 구하는 것이 아닌 Coarse grid 에서 근사값을 찾고, 그 결과를 finer grid 로 가져와 남은 오차(residual) 을 보정한다.

$$\text{solution} = \text{coarse solution} + \text{residual correction}$$

즉, 전채 해가 아니라 이미 있는 근사에서 residual 을 품으로써 수렴 속도가 빨라진다.

저자는 VLAD와 Multigrid에서 residual representation을 도입함으로써 문제를 직접 해결하는 대신 기준 해로부터의 차이만을 다루도록 재정식화하면 최적화가 단순해지고 수렴이 빨라진다는 점을 보여준다.

이러한 관찰을 바탕으로, 신경망에서도 전체 함수를 직접 학습하는 대신 입력에 대한 residual function을 학습하도록 문제를 재정식화한 것이 논문의 residual learning이며, 이는 구조적 트릭이 아니라 정당한 최적화 전략임을 주장한다.

Shortcuts Connections

Shortcut used researches

shortcut / skip connection 개념은 ResNet 논문의 저자가 처음 주장한 기법이 아니고 아이디어 자체는 오래되었다. shortcut 을 사용한 대표적인 사례 중 하나는 초기 MLP 에서 입력을 그대로 출력 그대로 보내는 선형 경로는 추가하는 것이었다. 하지만 이는 residual learning 의 목적은 아니었고, 학습 초기에 출력이 완전히 엉뚱해지는 것을 방지하기 위함이었다.

또 다른 사례는 auxiliary classifiers 로, deep network 에서 기울기 소실을 막기 위해 도입되었다. 중간 레이어에 보조 분류기를 추가하므로써 loss 를 중간에서 직접 걸어준다. 즉 gradient 를 강제로 중간까지 끌어오는 아이디어이다. 하지만 이는 학습 과정에서만 gradient를 보조적으로 공급하는 장치이며, inference 시의 함수 형태에는 아무런 제약도 가하지 않기 때문에 학습 타이밍의 테크닉에 그친다.

Centering layer responses 는 BN 과 유사한 방법론으로, activation 의 평균을 0 근처로 유지해 gradient 의 스케일을 안정화한다. 하지만 BN과 마찬가지로 통계적 안정화가 목적이기 때문에, 네트워크가 근사해야 할 함수 공간 자체는 변하지 않았으며, 단지 activation과 gradient의 분포만을 안정화하는 역할에 그친다.

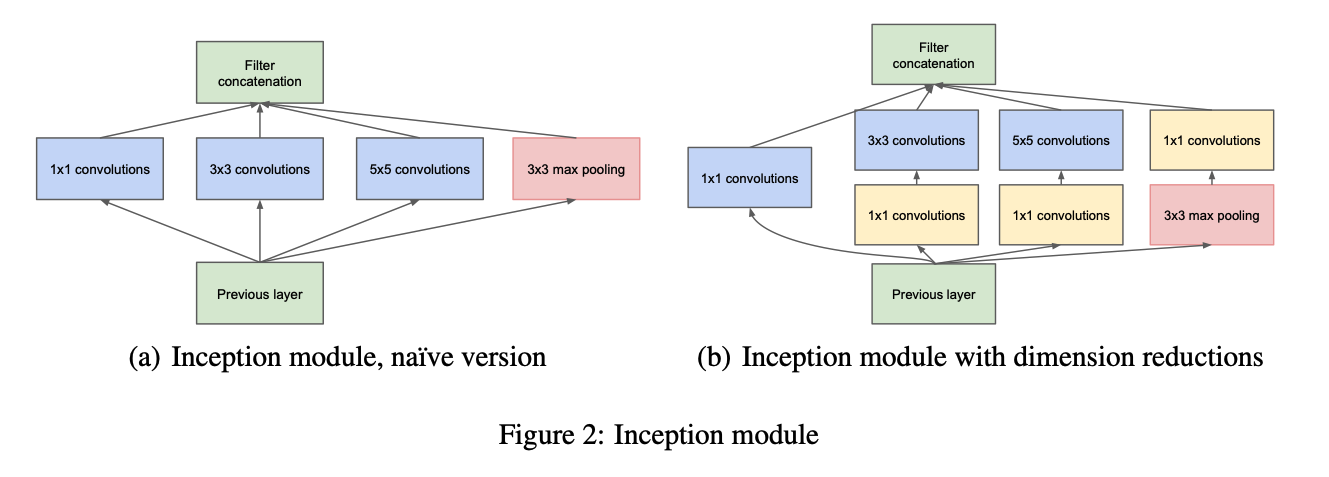
Inception network 에서도 비슷한 개념이 사용되었는데, 이전 레이어의 출력에서 1x1 conv, 3x3 conv, 5x5 conv, 3x3 max pool 의 누적 값을 연산에서 사용하는데, 이때 3x3 max pool 을 identity mapping 과 유사한 값으로 볼 수 있다. 하지만 3개 커널의 conv 결과와 pool 의 결과를 concatenation 한다는 점에서 완전한 shortcut 으로 볼 수 없고, pool 이 기본 해가 아니기 때문에 residual 만 학습한다는 제약은 없다.

Highway Network

highway network 는 깊은 네트워크에서의 vanishing gradient 문제를 해결하기 위해 연구된 주제로, ResNet 의 등장 배경과 가장 유사하다. 기본적인 접근은 vanishing gradient 문제를 정보 흐름을 제어하는 gate 로 해결하는 방식이다.

$$T(x) = \sigma(W_Tx+b_T)\\ y=T(x)H(x)+(1-T(x))x$$

$W_T, b_T$ 는 추가되는 파라미터로, 레이어를 항등함수로 사용할건지 (즉, 레이어를 건너뛸지) 혹은 레이어에서 값을 transfrom (레이어를 사용할지) 할건지 결정하게 된다.

$\sigma(x)\in(0, 1)$ 이고, $T(x)\approx1$ 이면 레이어를 사용, $T(x)\approx0$ 이면 레이어를 건너뛰게 된다. 즉, 필요한 레이어인지 아닌지 모델이 판단하게 하여 gradient 의 흐름을 유지한다.

하지만 ResNet 논문의 저자는 $T(x)$ 가 학습되는 값이라는 점에서 Highway Network는 항상 residual function을 학습하도록 구조적으로 보장하지 못한다고 지적한다. 또한 gating을 위한 추가 파라미터가 레이어마다 도입되므로, 네트워크 깊이가 증가할수록 파라미터 수와 연산량, 그리고 최적화 복잡도가 함께 증가한다.

Deep Residual Learning

Residual Learning

깊은 비선형 네트워크가 복잡한 함수 $H(x)$ 를 근사할 수 있다면, $H(x) - x$ 도 근사할 수 있어야한다. 즉 표현력의 관점에서 두 함수는 동일한 표현력 안에서 근사될 수 있다.

Introduce 에서 언급되었 듯 Residual Learning 은 레이어가 출력 전체를 만들지 않고, 입력에서 얼마나 바뀌는 지만 학습하게 하고, ( $y=x+F(x)$ ) 레이어가 항등함수로 학습되어야 한다면 여러 비선형 레이어가 정교하게 상쇄되어야 하는 것에 비해 $F(x)$ 의 가중치가 0이 되면 되므로 난이도가 훨씬 쉽다.

이러한 재정식화는 최적 함수가 항등함수 자체일 필요는 없지만, 항등함수에 가까운 경우 특히 효과적이다. 만약 최적 함수가 plain network의 기준점인 zero mapping보다 항등함수$(H(x)\approx x)$에 가깝다면, Residual Learning 이 최적화에 유리할 것 이다. 저자는 이후의 실험을 통해 실제로 학습된 residual function의 출력이 작다는 점을 보이며, 많은 경우 최적 함수가 identity mapping 근처에 위치함을 경험적으로 확인한다.

즉, 저자는 표현력은 동일하더라도 학습해야 할 함수를 어떻게 정의하느냐에 따라 최적화 난이도가 달라질 수 있으며, 특히 항등함수를 기준점으로 삼는 residual learning이 깊은 네트워크의 최적화를 크게 용이하게 만든다고 주장한다.

Identity Mapping by Shortcuts

Residual 은 네트워크 전체에 한번만 사용되는 것이 아니며 여러 레이어를 묶은 블록 단위로 반복 적용된다. 즉 $H(x)$ 는 몇개의 레이어가 학습해야할 목표 함수이며, 여기서 말하는 레이어는 전체 네트워크가 아니라 일부 블록을 의미한다.

$$y=F(x, \{W_i\})+x$$

에서, $x$ 는 블록의 입력, $y$ 는 블록의 출력, $F(x, \{W_i\})$ 은 모델이 학습해야할 residual mapping, $+x$ 은 항상 통과되는 identity shortcut 을 의미한다.

$F$ 는 보통 2~3개의 레이어로 이루어진 작은 서브 네트워크이며, 레이어가 2개라고 가정하면:

$$\sigma(x)=\text{max}(0, x)\\\quad\\ F=W_2\sigma(W_1x)\\\quad\\y = \sigma(F(x) + x)$$

이다. $F + x$ 이후 한번의 활성함수를 거친 $\sigma(F + x)$ 가 블럭의 출력이 된다. (second nonlinearity after the addition**)**

이 식의 shortcut connection 은 계산 복잡도를 올리지 않는다. 이는 실용적일 뿐만 아니라 Plain Network 와 Residual Network 를 비교하는 데 있어서도 중요하다. 무시할 수 있을 정도의 원소별 덧셈을 제외하고, 파라미터 수, 깊이, 너비, 계산 비용이 동일한 공정한 비교가 가능해진다.

$F + x$ 가 원소별 덧셈이기 때문에 두 값의 차원은 동일해야 한다. 만약 그렇지 않을 경우 선형 투영 $W_s$ 를 수행하여 차원을 맞출 수 있다.

$$y=\sigma(F(x, \{W_i\})+W_sx)$$

실험을 통해 $F$ 와 $x$ 의 차원을 같게 만들어도 충분히 효과적임이 확인되었으므로 $W_s$는 차원을 맞춰야 하는 경우에만 사용한다. residual 함수 $F$의 형태는 유연하다. 본 논문의 실험에서는 두 개 또는 세 개의 층을 갖는 함수 $F$ 만을 사용하지만 그보다 많은 층을 사용하는 것도 가능하다.

하지만 만약 레이어 하나로만 구성하는 경우 Plain Network 와 유사해진다. $(y = \sigma(W_1x) + x)$ 이 경우 특별한 이점을 관측할 수 없다.

위 식들은 표기의 단순함을 위해 FC 층을 기준으로 설명되었지만 Convolution 층에도 그대로 적용될 수 있다. $F(x, \{W_i\})$ 는 여러개의 Convolution 층으로 나타낼 수 있고, 원소별 덧셈 $(+x)$ 은 두 개의 feature map 에 대해 채널별로 수행된다.

VGG, Plain Network and Residual Network

저자는 여러 종류의 plain 네트워크와 residual 네트워크를 실험했고, 깊어질수록 plain 네트워크는 training error 자체가 증가하는 반면 residual 네트워크는 안정적으로 최적화된다는 일관된 현상을 관찰했다.

이러한 차이가 다른 요인 때문이라는 반박을 차단하기 위해, “Residual Network는 깊은 네트워크에서도 학습에 유리하다”는 주장을 검증하기에 충분히 강한 Plain Network를 의도적으로 설계하였다.

• VGG 의 철학을 따른다. → 이미 검증된 깊이의 CNN 구조를 유지한다.
• 모든 Conv 레이어에서 커널 차원을 3x3 로 고정한다. → 레이어의 깊이만이 핵심 변수로 남도록 한다.
• feature map 해상도가 내려가면 채널 수를 올린다. → 레이어 간 연산양(FLOPs)을 일관되도록 유지한다.
• 다운샘플링은 pooling 대신 stride conv 로 한다 → 사람이 네트워크의 구조에 개입하지 않는다.

즉 저자는 ResNet 의 효용을 regularization도, 파라미터 수도, 연산량도 아니라 최적화 가능한 구조 때문임을 증명하려고 한다.

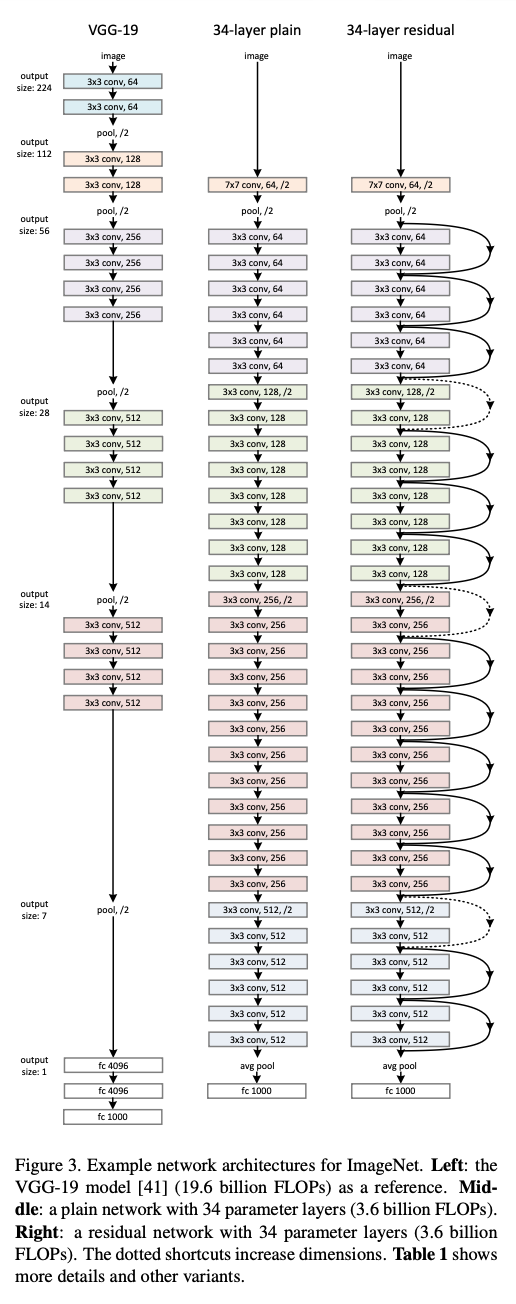
구성한 Plain Network 에 Shortcut 을 추가한 Residual Network 도 구성한다. 이 때 Block 의 입력과 출력의 채널 수가 다를 때 두가지 옵션을 테스트한다.

• Option A - 채널 증가 시 shortcut은 identity를 유지하고, 부족한 채널만 0으로 padding

  $$x \rightarrow [x, 0]$$

• Option B - 차원을 맞추기 위해 1x1 conv 를 통해 선형 투영을 수행한다.

  $$x \rightarrow W_s^{1\times1}(x)$$

두 옵션 모두, shortcut 이 해상도를 건너뛰어야 할 때는 stride of 2 로 구현한다.

즉, 동일한 해상도 간 연결:

$$x \in \mathbb{R}^{H\times W\times C}\\ F(x)\in \mathbb{R}^{H\times W\times C}\\ y=F(x)+x$$

해상도가 바뀌는 지점 ($\frac{1}{2}$):

$$x \in \mathbb{R}^{H\times W\times C} \\F(x)\in \mathbb{R}^{\frac{H}{2}\times \frac{W}{2}\times 2C} \\ \quad\\ \tilde{x} =\begin{cases}[\text{stride}_{2}(x), 0] & \text{(Option A)} \\W_s^{1\times1,\;\text{stride}=2}(x) & \text{(Option B)}\end{cases} \\\quad\\ \tilde{x}\in \mathbb{R}^{\frac{H}{2}\times \frac{W}{2}\times 2C} \\ y = F(x) + \tilde{x}$$

Implementation Details

저자는 구성한 네트워크를 ImageNet 으로 실험하기 위해 다음과 같이 셋업하였다:

| Data Augmentation | 1. Scale Augmentation

• 이미지의 짧은 변을 256 ~ 480 사이에서 랜덤하게 resize

2. Random crop + flip

• resized 이미지에서 224x224 를 랜덤 crop 하고 mean subtraction

3. Color Augmentation

항목	세부 내용
Color Augmentation	AlexNet 계열에서 도입된 색상 노이즈 적용
Batch Normalization	각 convolution 뒤, activation 앞에 BN 적용
Weight Initialization	ReLU 친화적 He initialization 사용
Optimization & Batch Size	mini-batch 256의 SGD 사용, learning rate 0.1에서 시작, 성능 정체 시 1/10로 감소, momentum 0.9 적용
Training Length	최대 600k iteration까지 학습
Regularization	weight decay 1e-4

• 10-crop testing: CNN 기반 이미지 분류에서 테스트 시점에 입력을 여러 번 변형해서 추론하고, 그 결과를 평균(또는 투표)하는 기법

Experiments

ImageNet Classification

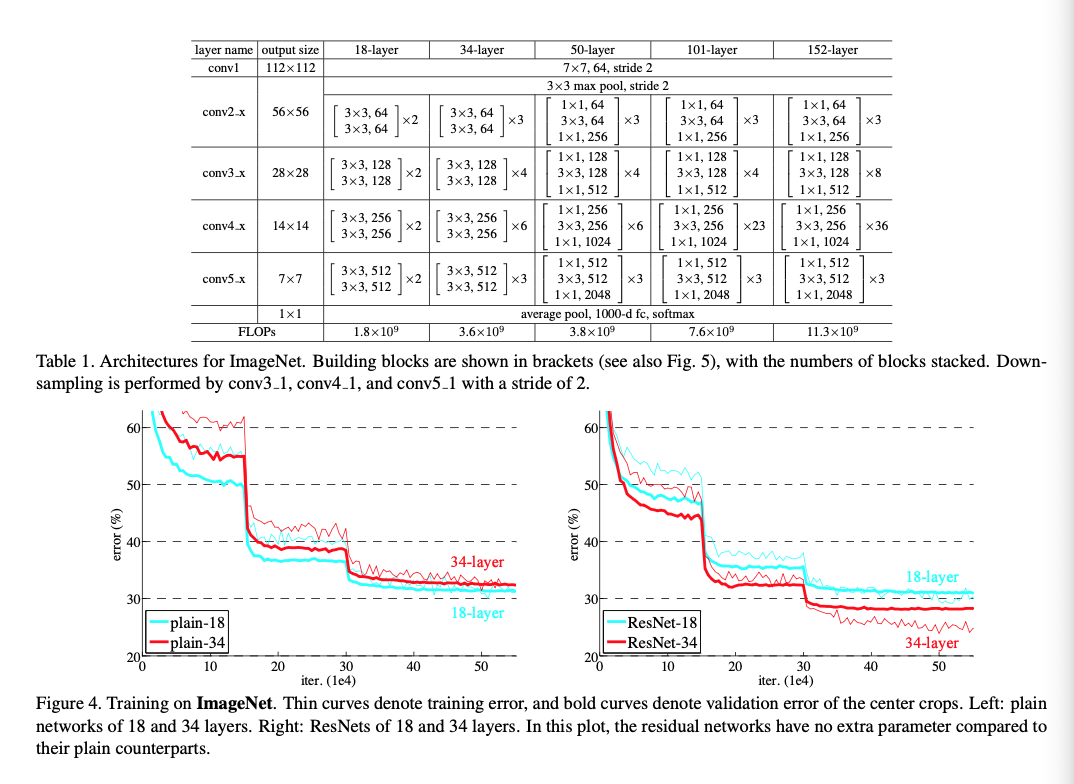
Plain Networks

저자는 residual 연결이 없는 plain 네트워크에서 깊이만 증가시켰을 때 어떤 현상이 발생하는지를 확인하기 위해, 구조는 거의 동일하고 깊이만 다른 18-layer와 34-layer plain 네트워크를 비교하였다. 실험 결과, 더 깊은 34-layer plain 네트워크가 오히려 18-layer 네트워크보다 validation error가 더 높게 나타났다. 이 차이가 과적합 때문인지 확인하기 위해 학습 과정 전반의 training/validation error를 분석한 결과, 34-layer 모델은 학습 초기부터 종료까지 training error 자체가 더 높게 유지되는 degradation 문제를 보였다.

저자는 깊은 plain 네트워크에서 나타나는 최적화 어려움이 단순히 gradient vanishing 때문이라고 보기는 어렵다고 주장한다. 네트워크는 모두 Batch Normalization을 사용해 학습되었으며, BN은 순전파 과정에서 활성값의 분산을 안정적으로 유지해 신호가 사라지는 현상을 완화한다. 더 나아가 저자는 BN을 사용한 상태에서 역전파되는 gradient의 크기를 실제로 관측해 보았고, 그 값들이 정상적인 범위에 있음을 확인하였다.

따라서 gradient가 소실되어 학습이 실패하는 상황은 아니라는 결론에 이른다. 실제로 34-layer plain 네트워크는 비록 얕은 모델보다 성능이 낮지만 완전히 학습이 붕괴된 것은 아니며, 이는 최적화가 어느 정도는 작동하고 있음을 보여준다. 저자는 대신 깊은 plain 네트워크가 깊이에 따라 수렴 속도가 급격히 느려지는 문제를 겪고 있을 가능성을 제기하며, 이러한 최적화 난이도의 근본 원인은 향후 연구 과제로 남긴다.

Residual Network

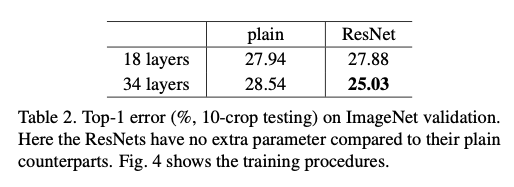
저자는 이제 residual network 를 평가한다. 기본 아키텍쳐는 이미 언급하였듯 plain 네트워크와 동일하며, shortcut 의 사용 여부만 다르다. 해상도나 채널 수가 증가하는 지점에서는 Option A 를 사용하여 테스트한다. Option A 를 사용할 경우, plain network 와 residual network 의 파라미터 수는 완벽히 동일하게 된다. (Option B 사용 시 $W_s$ 가 추가됨)

실험 결과는 plain 네트워크와는 달리 상황이 완전히 뒤집혀, 34-layer ResNet이 18-layer ResNet보다 더 좋은 성능을 보인다(약 2.8% 향상). 둘째이자 더 중요한 점은 34-layer ResNet이 training error 자체가 크게 낮아졌고, 그 성능이 validation 데이터에도 잘 일반화된다는 것이다. 이는 앞서 plain 네트워크에서 관찰되었던 degradation 문제가 residual learning을 통해 효과적으로 해결되었음을 의미한다.

34-layer 기준에서 residual 구조를 적용한 ResNet은 plain 네트워크보다 training error를 효과적으로 낮추며, 그 결과 top-1 error를 크게 개선한다. 이는 residual learning이 깊은 네트워크에서도 최적화를 가능하게 만들어 깊이 증가가 실제 성능 향상으로 이어질 수 있음을 보여준다. 반면 18-layer처럼 상대적으로 얕은 네트워크에서는 plain과 residual의 최종 정확도 차이는 거의 없지만, ResNet은 학습 초반 수렴 속도를 개선해 최적화를 더 빠르고 안정적으로 만드는 역할을 한다.

Identity vs Projection Shortcuts

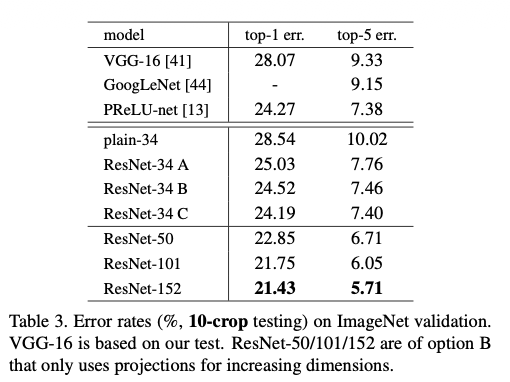
저자는 identity shortcut만으로도 깊은 네트워크의 학습이 충분히 개선된다는 점을 보인 뒤, projection shortcut의 필요성을 추가로 검증한다. zero-padding 기반 identity shortcut(Option A), 해상도 변경 지점에서만 projection을 쓰는 방식(Option B), 모든 shortcut을 projection으로 사용하는 방식(Option C)을 비교한 결과, 세 옵션 모두 plain 네트워크보다 크게 우수했으며, 성능 차이는 매우 작았다. B와 C가 A보다 약간 나은 성능을 보이긴 했지만, 이는 zero-padding된 채널이 residual 학습을 하지 못하는 점이나 projection으로 인한 추가 파라미터 효과로 설명 가능하다.

저자는 메모리 사용량과 연산량, 모델 크기를 줄이기 위해 이후의 실험에서는 Option C를 사용하지 않는다. 특히 identity shortcut은 이후에 도입될 bottleneck 구조에서도 모델 복잡도를 증가시키지 않는다는 점에서 중요하다.

Bottleneck Architectures

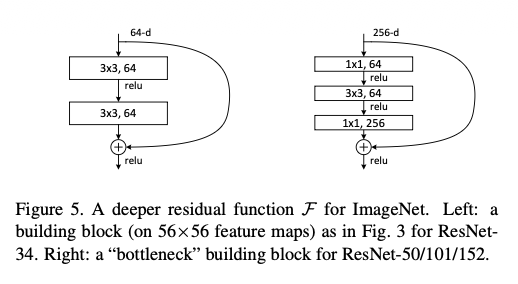
더 깊은 ResNet을 효율적으로 학습하기 위해 저자는 bottleneck 구조를 도입했으며, 이는 1×1–3×3–1×1 convolution으로 구성되어 비싼 3×3 연산을 저차원 공간에서만 수행하도록 만든 설계다. 이 구조는 레이어 수를 늘리면서도 연산량을 기존 설계와 비슷하게 유지할 수 있게 해준다. 이러한 bottleneck 구조에서는 shortcut이 고차원 feature에 직접 연결되므로, projection shortcut을 사용하면 연산량과 파라미터 수가 크게 증가한다. 따라서 파라미터와 연산 비용이 없는 identity shortcut (Option A) 이 bottleneck 구조에서 특히 중요하며, 이를 통해 매우 깊으면서도 효율적인 ResNet 모델을 구성할 수 있다.

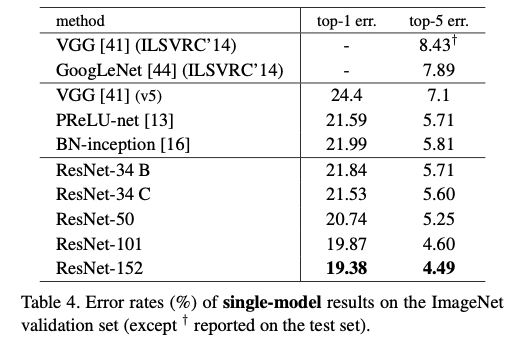
또한 bottleneck 구조를 도입해 50, 101, 152-layer ResNet을 구성한 결과, 네트워크 깊이를 크게 늘렸음에도 연산량은 VGG보다 낮은 수준으로 유지되었고, degradation 문제 없이 깊이 증가가 곧바로 정확도 향상으로 이어졌다.

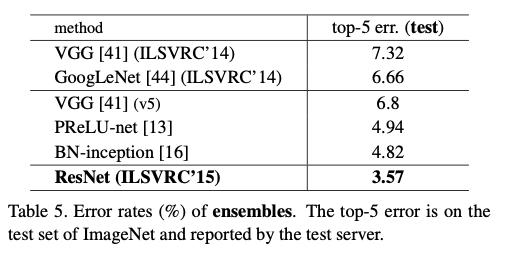
ResNet은 단일 모델만으로도 기존 최고 성능의 앙상블 모델을 뛰어넘는 결과를 달성했으며, 특히 152-layer ResNet은 단일 모델 기준 top-5 error 4.49%로 당시 state-of-the-art를 갱신했다. 서로 다른 깊이의 ResNet들을 앙상블로 결합하면 top-5 error를 3.57%까지 낮출 수 있었고, 이 결과로 ResNet은 ILSVRC 2015 이미지 분류 대회에서 우승을 차지했다.

CIFAR-10

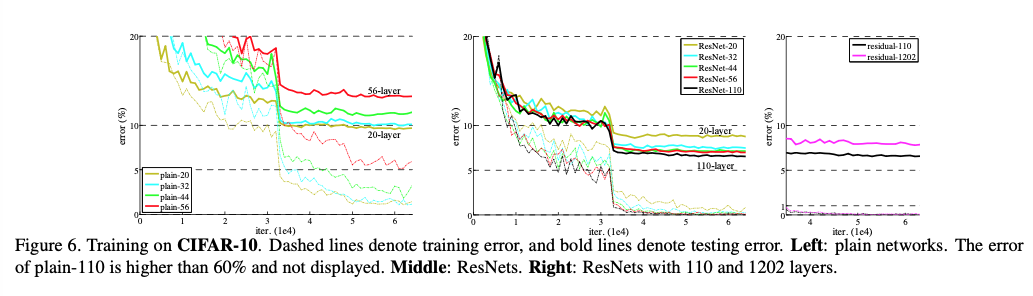
저자는 CIFAR-10 데이터셋에서 추가 실험을 수행하며, 이 실험의 목적은 최고 성능을 달성하는 것이 아니라 매우 깊은 네트워크가 어떻게 학습되는지를 관찰하는 데 있다. 이를 위해 의도적으로 단순한 plain 및 residual 아키텍처를 사용하고, 입력은 32×32 이미지에 대해 mean subtraction 만 수행한다. 네트워크는 3x3 convolution을 기본으로 하여 feature map 크기 32, 16, 8의 세 단계로 구성되며, 각 단계마다 $2n$개의 레이어를 쌓아 전체 깊이를 $6n+2$로 조절한다. 다운샘플링은 stride 2 convolution으로 수행되고, 마지막에는 global average pooling과 10-class 분류기를 둔다. 이 설정을 통해 저자는 구조적 트릭의 영향을 최소화한 상태에서, 네트워크 깊이가 증가할 때 plain 네트워크와 residual 네트워크의 추이를 직접 비교한다.

네트워크 깊이는 $n = {3,5,7,9}$ 로 조절해 20층부터 56층까지 확장한다. 실험 결과, plain 네트워크는 깊이가 증가할수록 training error가 오히려 커지는 degradation 현상을 보였으며, 이는 ImageNet이나 MNIST에서도 관찰된 것과 동일한 근본적인 최적화 문제임을 시사한다. 반면 ResNet은 깊이가 깊어질수록 이러한 최적화 어려움을 극복하고, 일관된 정확도 향상을 보인다. 즉, CIFAR-10에서도 residual 구조는 깊은 네트워크의 학습을 가능하게 하며, 깊이 증가의 이점을 안정적으로 실현시킨다는 점이 확인된다.

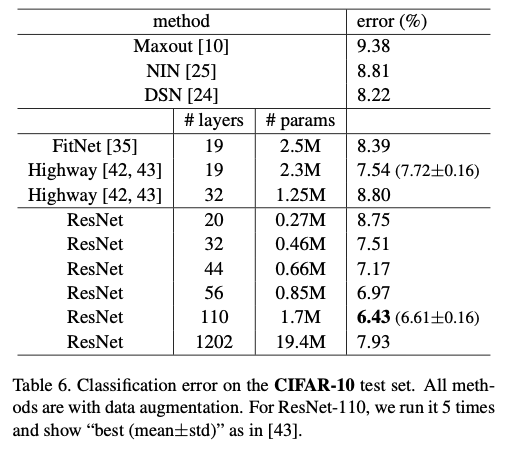
저자는 $n=18$ 까지 확장하여 테스트한다. 아주 깊은 110-layer 네트워크에서도 residual 구조는 간단한 warm-up만으로 안정적인 학습을 가능하게 하며, 적은 파라미터로도 최고 수준의 성능을 달성한다.

Analysis of Layer Response

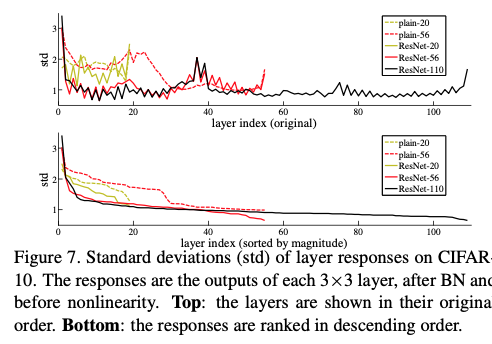
저자는 각 3x3 convolution 레이어의 출력값 std 을 분석한다. 여기서 말하는 레이어 응답은 BN 이후, ReLU나 shortcut 덧셈 이전의 값으로, ResNet에서는 곧 residual function $F(x)$ 의 크기를 의미한다.

레이어 응답의 std 라고 하면 레이어 유닛들의 응답값에 대한 분포를 의미하지만:

$$\sigma = \sqrt{\frac{1}{N}\sum^N_{i=1}(F(x)_i-\mu)^2}$$

에서, BN에 의해 $\mu \approx 0$ 이므로, $\sigma \approx \sqrt{\frac{1}{N}\sum_{i=1}^{N}F(x)_i^2}$ 이 되므로 레이어 응답의 strength 로 볼 수도 있다.

분석 결과, ResNet의 레이어 응답은 대응되는 plain 네트워크보다 전반적으로 더 작은 값을 가지며, 이는 residual 함수가 원래의 non-residual function 에 비해 0에 더 가까운 값을 학습한다는 저자의 가정을 뒷받침한다. 또한 ResNet-20, 56, 110을 비교해 보면, 네트워크가 더 깊어질수록 각 레이어의 응답 크기가 더 작아지는 경향이 관찰된다. 이는 ResNet이 깊어질수록 개별 레이어가 입력 신호를 크게 변형하기보다는, 아주 작은 수정만을 점진적으로 누적하는 방식으로 동작한다는 것을 의미한다.

즉, 저자가 의도한 최적화 경로로 실제로 SGD가 움직였다.

Over 1000 ResNet Layers

저자는 CIFAR-10에서 residual 구조의 한계를 시험하기 위해 $n = 200$, 즉 1202-layer에 달하는 초심층 ResNet까지 실험을 확장한다. 이 모델은 학습 과정에서 최적화 문제를 전혀 보이지 않으며, training error를 0.1% 이하로 낮출 수 있을 정도로 안정적으로 수렴한다. 이는 residual 구조가 깊이가 1000층을 넘어가더라도 최적화 자체에는 본질적인 한계가 없음을 보여준다. 다만 테스트 성능에서는 1202-layer 모델이 110-layer 모델보다 오히려 나쁜 결과를 보이는데, 두 모델의 training error가 비슷하다는 점에서 이를 과적합 문제로 해석한다.