10x Faster C++ String Split

지난 포스트들에서 SIMD 인스트럭션과 SIMD 를 string 에 활용하는 법에 대해 포스팅을 했었는데요, 오늘은 @ashvardanian의 splitting-strings-cpp 포스팅을 리뷰하면서 split 함수를 구현해보려고 합니다.

특히 저의 경우 Python 에서 제일 많이 사용하는 함수 중 하나가 split 입니다.

이 포스트에서는 문자열을 나누는 여러 방법을 살펴보고, 그 중 가장 빠른 방법과 그 구현, 장단점을 살펴보려고 합니다.

Problem Definition

문제를 정의 해봅시다. split 은 바이트 시퀀스와 delimiter 문자 집합이 주어졌을 때, 이 delimiter 를 기준으로 문자열을 나누는 함수입니다.

일반적으로 공백을 기준으로 문자열을 나누죠. C언어의 로케일에서는 "\f", "\r", "\n", "\t", "\v", " " 의 6개 문자가 공백 문자로 정의되어 있습니다.

보통 " " 하나만을 delimiter 로 사용하는 경우가 많습니다. 하지만 파싱을 하다 보면 XML 의 <, >, JSON 의 {, }, [, ] 등의 2개 이상 문자들을 delimiter 로 사용해야 하는 경우가 있습니다.

Solution 1: using std::string_view::find_first_of

template <typename callback_type_>
void split(std::string_view str, std::string_view delimiters,
           callback_type_ && callback) {
    std::size_t pos = 0;
    while (pos < str.size()) {
        auto const next_pos = str.find_first_of(delimiters, pos);
        callback(str.substr(pos, next_pos - pos));
        pos = next_pos == std::string_view::npos ? str.size()
                                                 : next_pos + 1;
    }
}

std::string_view::find_first_of 는 문자열에서 주어진 문자 집합에 포함된 문자가 처음으로 나타나는 위치를 찾아줍니다.

내부적으로 순차 탐색을 하는데, delimiters 의 길이가 늘어나면 성능이 확 떨어지죠.

굳이 시간 복잡도로 보면 O(n * len(delimiters)) 라고 볼 수 있습니다.

Solution 2: using std::find_if and lambda

만약 delimiter 를 판단하는 커스텀 람다 함수를 전달하면, O(n) 으로 해결할 수 있겠습니다.

template <typename callback_type_, typename predicate_type_>
void split_with_predicate(std::string_view str, predicate_type_ && is_delimiter, callback_type_ && callback) {
    std::size_t pos = 0;
    while (pos < str.size()) {
        auto const next_pos = std::find_if(str.begin() + pos, str.end(), is_delimiter) - str.begin();
        callback(str.substr(pos, next_pos - pos));
        pos = next_pos == str.size() ? str.size() : next_pos + 1;
    }
}

Benchmark: solution 1 vs solution 2

inline bool is_delimiter(char c) {
    return c == ' ' || c == '\t' || c == '\n' || c == '\r' || c == '\f' || c == '\v';
}

static void BM_Split(benchmark::State& state) {
    std::string text = "This is a sample text to be split using delimiters.";
    for (auto _ : state) {
        split(text, " \t\n\r\f\v", [](std::string_view) {
            benchmark::DoNotOptimize(1);
        });
    }
}

static void BM_SplitWithPredicate(benchmark::State& state) {
    std::string text = "This is a sample text to be split using delimiters.";
    for (auto _ : state) {
        split_with_predicate(text, is_delimiter, [](std::string_view) {
            benchmark::DoNotOptimize(1);
        });

    }
}

BENCHMARK(BM_Split);
BENCHMARK(BM_SplitWithPredicate);

BENCHMARK_MAIN();

-O0 Benchmark	Time	CPU	Iterations
BM_Split	1678 ns	1678 ns	416055
BM_SplitWithPredicate	569 ns	568 ns	1226564

-O3 Benchmark	Time	CPU	Iterations
BM_Split	41.8 ns	41.8 ns	16705647
BM_SplitWithPredicate	37.2 ns	37.2 ns	18774709

컴파일러 최적화 옵션에 따라 성능 차이가 있지만, BM_SplitWithPredicate 가 BM_Split 보다 빠르다는 것을 확인할 수 있습니다.

Solution 3: using character bit-set

결국 문자열을 나누는 로직의 첫번쨰 과정은 문자열 내부의 delimiter 위치를 찾는 것이고, 문제를 더 잘게 쪼개면 문자열 내부의 문자가 delimiter 인지 아닌지를 판단하는 것입니다.

문자가 delimiter 인지 아닌지를 판단하는 것을 비트 연산으로 접근해보곘습니다.

char set[32] = {0};

const char* delimiters = " \t\n\r\f\v";

for (char c : std::string_view(delimiters)) {
    set[c >> 3] |= 1 << (c & 7);
}

bool is_delimiter(char c) {
    return set[c >> 3] & (1 << (c & 7));
}

set 은 문자 집합을 비트 플래그로 표현한 집합입니다. 8비트 자료형인 char 가 32개 있으니, 총 256비트의 비트 플래그를 사용할 수 있습니다.

즉 만약 A 가 delimiter 라면, 정수로 해석한 값은 65이므로 set 의 65 >> 3 인덱스의 65 & 7 번째 비트가 1이 됩니다.

set[0]  = 0b00000000;
set[1]  = 0b00000000;
...
set[8]  = 0b00000010; // 'A' 의 비트 플래그가 켜짐
...
set[31] = 0b00000000;

is_delimiter 함수는 문자를 정수로 해석한 값을 8로 나눈(c / 8 == c >> 3) 몫을 인덱스로 사용합니다. 그리고 나머지(c & 7 == c % 8) 를 비트 마스크로 사용합니다.

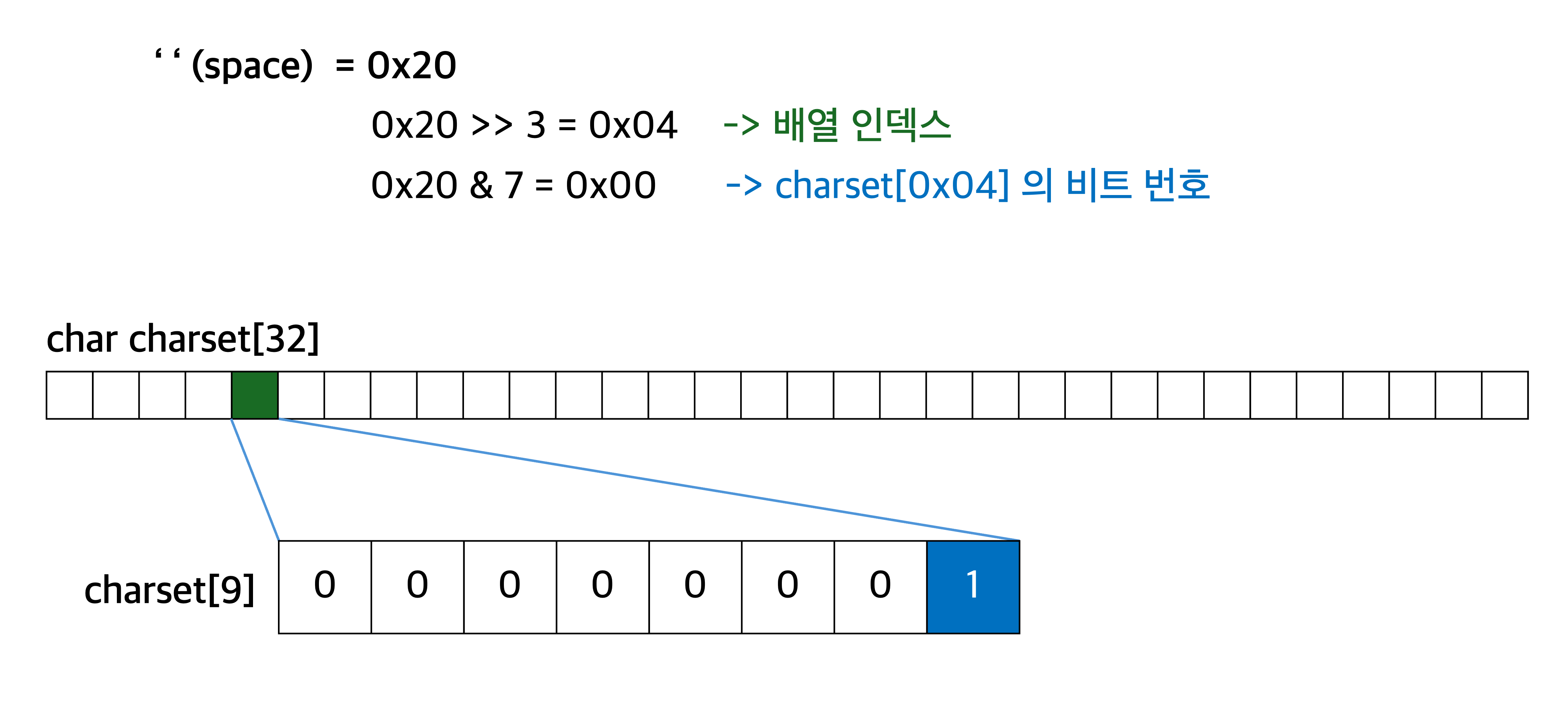
여기서 모듈러연산이 비트 연산으로 대체되는데, c % n 에서 n 이 2의 거듭제곱이라면 c & (n - 1) 로 대체할 수 있습니다.

두 연산이 본질적으로 “c의 하위 k 비트를 분리해내는” 동일한 작업을 수행하기 때문입니다.

n 이 2의 거듭제곱 (2^k) 이라면, 2진수로 표현했을 때 단 하나의 비트만 1이고, n - 1 의 경우 하위 k 개 비트가 1이 됩니다.

0b10000000 -> 2^7
0b01111111 -> 2^7 - 1

c & 0b01111111 == c & 0b11111111

즉 k 번째 비트까지 마스킹하는 것은 본질적으로 c % 2^k 와 동일합니다.

다시 문자열 비교로 돌아와서, set 은 메모리 지역성이 좋은 배열이므로, 캐시 히트율이 높을 것이고 정수 연산이 아닌 비트 연산을 사용하므로 더 빠를 것입니다. L1 캐시에 상주할 가능성이 매우 높죠.

이제 == 연산자를 반복적으로 사용하는 이전의 방법 대신 방금 구현한 비트연산 기반 함수를 사용하여 벤치마크 해보겠습니다.

inline bool is_delimiter(char c) {
    return c == ' ' || c == '\t' || c == '\n' || c == '\r' || c == '\f' || c == '\v';
}

static void BM_SplitWithPredicate(benchmark::State& state) {
    std::string text = "This is a sample text to be split using delimiters.";
    for (auto _ : state) {
        split_with_predicate(text, is_delimiter, [](std::string_view) {
            benchmark::DoNotOptimize(1);
        });

    }
}

static void BM_SplitWithPredicate_CharSet(benchmark::State& state) {
    char set[32] = {0};
    const char* delimiters = " \t\n\r\f\v";

    for (char c : std::string_view(delimiters)) {
        set[c >> 3] |= 1 << (c & 7);
    }

    auto is_delimiter_char_set = [&](char c) {
        return set[c >> 3] & (1 << (c & 7));
    };

    std::string text = "This is a sample text to be split using delimiters.";
    for (auto _ : state) {
        split_with_predicate(text, is_delimiter_char_set, [](std::string_view) {
            benchmark::DoNotOptimize(1);
        });
    }

}

Benchmark	Time	CPU	Iterations
BM_SplitWithPredicate	44.8 ns	44.8 ns	15622768
BM_SplitWithPredicate_CharSet	32.0 ns	32.0 ns	21921995

확실히 빠른 것을 알 수 있습니다. 28% 정도 빠르네요.

Solution 4: using SIMD

지금까지 solution 3 의 아이디어에 SIMD 를 적용해보겠습니다.

비트 마스크 기반 비교 로직을 동시에 여러 문자에 대해 적용하면 더 빨라지겠죠? ARM NEON 기반으로 구현해보겠습니다.

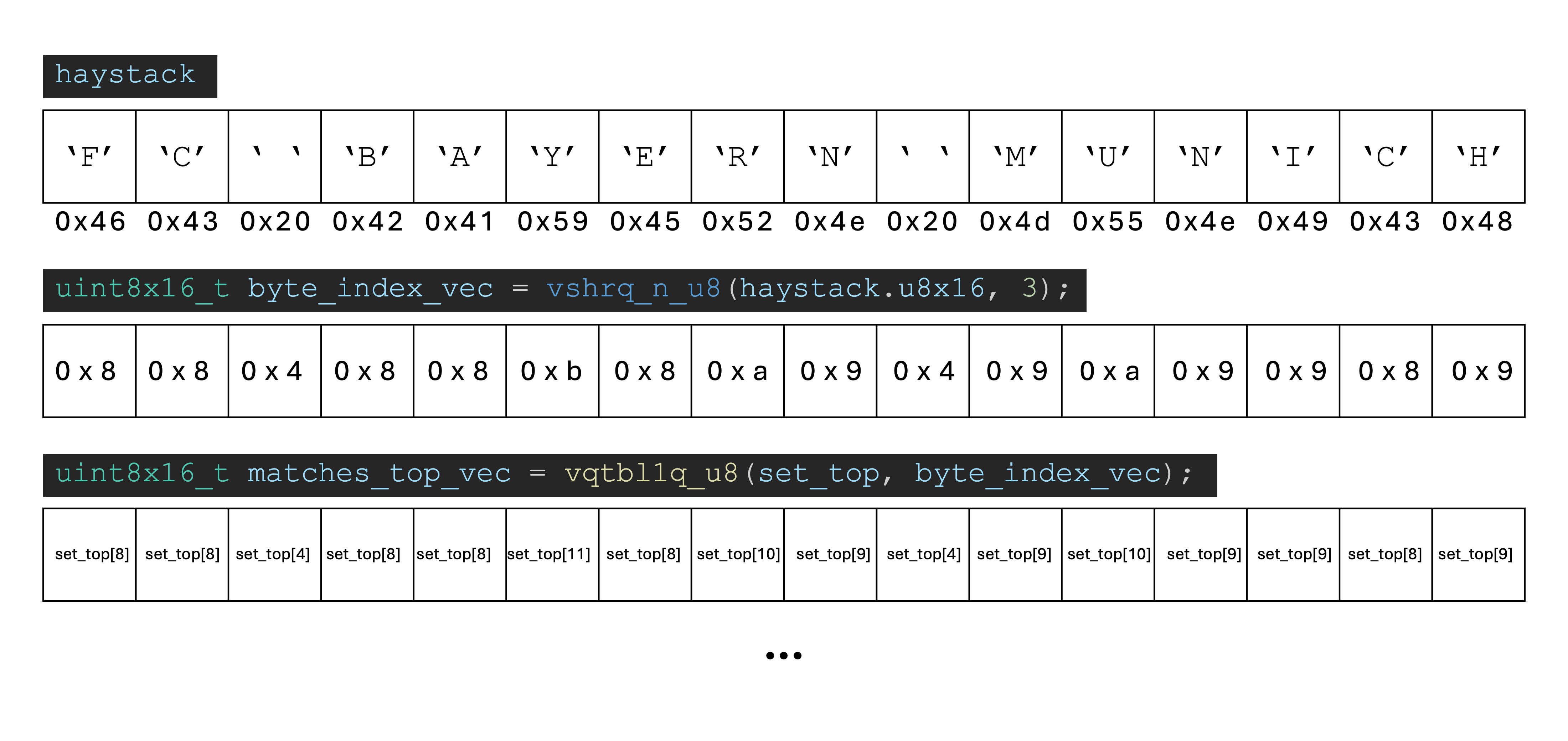
이 사진처럼 원리 자체는 똑같지만, 16개의 문자를 한번에 처리한다는 것이 포인트입니다.

16개씩 쭉 진행하다가 자투리 부분은 스칼라로 처리하는 구현입니다.

#include <arm_neon.h>
#include <string_view>

typedef union u128_vec_t {
  uint8x16_t u8x16;
  uint16x8_t u16x8;
  uint32x4_t u32x4;
  uint64x2_t u64x2;
  std::uint64_t u64s[2];
  std::uint32_t u32s[4];
  std::uint16_t u16s[8];
  std::uint8_t u8s[16];
} u128_vec_t;

std::uint64_t _find_charset_neon_register(u128_vec_t haystack,
                                          uint8x16_t set_top,
                                          uint8x16_t set_bottom) {
  /* haystack 은 "ABCDEFGHIJKLMNOP" 라고 가정 */

  uint8x16_t byte_index_vec = vshrq_n_u8(haystack.u8x16, 3);
  /* c >> 3 을 8비트 데이터 16개에 대해 동시에 수행
     즉, 각 바이트의 인덱스가 계산된다.
     - byte_index_vec 는 [65 >> 3, 66 >> 3, 67 >> 3, ... ] 이 된다. */

  uint8x16_t byte_mask_vec =
      vshlq_u8(vdupq_n_u8(1),
               vreinterpretq_s8_u8(vandq_u8(haystack.u8x16, vdupq_n_u8(7))));
  /* 1 << (c & 7) 을 8비트 데이터 16개에 대해 동시에 수행 */

  uint8x16_t matches_top_vec = vqtbl1q_u8(set_top, byte_index_vec);
  /* set_top 에서 바이트 단위 인덱싱
     - matches_top_vec 는
       [set_top[65 >> 3], set_top[66 >> 3], set_top[67 >> 3], ... ] 이 된다.
     - 즉, byte_index_vec 에 대응하는 set_top 의 값을 가져온다. */

  uint8x16_t matches_bottom_vec =
      vqtbl1q_u8(set_bottom, vsubq_u8(byte_index_vec, vdupq_n_u8(16)));
  /* - set_bottom 에 대해서도 바이트 단위 인덱싱 수행
     - 16을 빼는 이유는 set_bottom 의 바이트 인덱스가 0부터 시작하기 때문이다.
     - 똑같이 matches_bottom_vec 는
       [set_bottom[(65 >> 3) - 16], set_bottom[(66 >> 3) - 16], ... ] 이 된다.
     - vqtbl1q_u8 은 범위를 넘어가면 0을 반환한다. (65 >> 3) - 16 은 범위를
       넘어가므로 (underflow), matches_bottom_vec 는 모두 0이 된다. */

  uint8x16_t matches_vec = vorrq_u8(matches_top_vec, matches_bottom_vec);
  /* set_top 과 set_bottom 의 결과를 합친다. */

  matches_vec = vtstq_u8(matches_vec, byte_mask_vec);
  /* matches_vec 와 byte_mask_vec 를 비교한다. */

  return vget_lane_u64(vreinterpret_u64_u8(
                           vshrn_n_u16(vreinterpretq_u16_u8(matches_vec), 4)),
                       0) &
         0x8888888888888888ull;
  /* 1. vreinterpretq_u16_u8 로 matches_vec 를 16비트 데이터 8개로 재해석한다.
     2. 비트를 오른쪽으로 4비트 시프트 후, 하위 8비트만 취한다.
        (예시: static_cast<uint8_t>(n >> 4))
     3. vreinterpret_u64_u8 로 64비트 데이터 1개로 재해석한다.
     4. vget_lane_u64 으로 그 값을 스칼라로 가져온다.
     5. 마스킹 연산으로, 4비트 마다의 최상위 비트만 남긴다. */
}

template <typename callback_type_>
void split_neon(std::string_view str, std::string_view delimiters,
                callback_type_ &&callback) {
  std::uint8_t charset[32] = {0};
  for (char c : delimiters) {
    charset[c >> 3] |= 1 << (c & 7);
  }
  const uint8x16_t set_top_vec_u8x16 = vld1q_u8(charset);
  const uint8x16_t set_bottom_vec_u8x16 = vld1q_u8(charset + 16);

  std::uint64_t matches = 0;
  std::uint64_t bit_pos = 0;
  std::uint64_t char_pos = 0;
  u128_vec_t haystack_vec;

  const std::size_t length = str.length();
  std::size_t last_pos = 0;

  /* 16바이트 청크 단위로 처리한다. */
  for (std::size_t i = 0; i < length; i += 16) {
    haystack_vec.u8x16 =
        vld1q_u8(reinterpret_cast<const unsigned char *>(str.data() + i));

    matches = _find_charset_neon_register(haystack_vec, set_top_vec_u8x16,
                                          set_bottom_vec_u8x16);

    while (matches) {
      bit_pos = __builtin_ctzll(matches);
      char_pos = i + bit_pos / 4;
      callback(str.substr(last_pos, char_pos - last_pos));
      last_pos = char_pos + 1;
      matches &= ~(1ull << bit_pos);
    }
  }

  /* 16바이트 청크 단위로 처리하지 못한 나머지 부분은 스칼라로 처리한다. */
  if (length & 15) {
    std::size_t pos = length - (length & 15);
    while (pos < length) {
      if (charset[str[pos] >> 3] & (1 << (str[pos] & 7)) || pos == length - 1) {
        callback(str.substr(last_pos, pos - last_pos));
        last_pos = pos + 1;
      }
      pos++;
    }
  }
}

코드에 최대한 주석을 달아봤습니다. 꼼꼼히 읽어보시면 이해가 어렵지 않을 것 같습니다.

Benchmark

std::string generate_random_string(std::size_t length) {
    srand(0xcafe);
    std::string str(length, ' ');
    for (std::size_t i = 0; i < length; i++) {
        str[i] = 'a' + rand() % 26;
        i += rand() % 2;
    }
    return str;
}

이 코드로 문자 1000개 정도의 문자열을 생성하여 벤치마크를 진행했습니다. (std::mt19937 를 쓸 걸 그랬네요.)

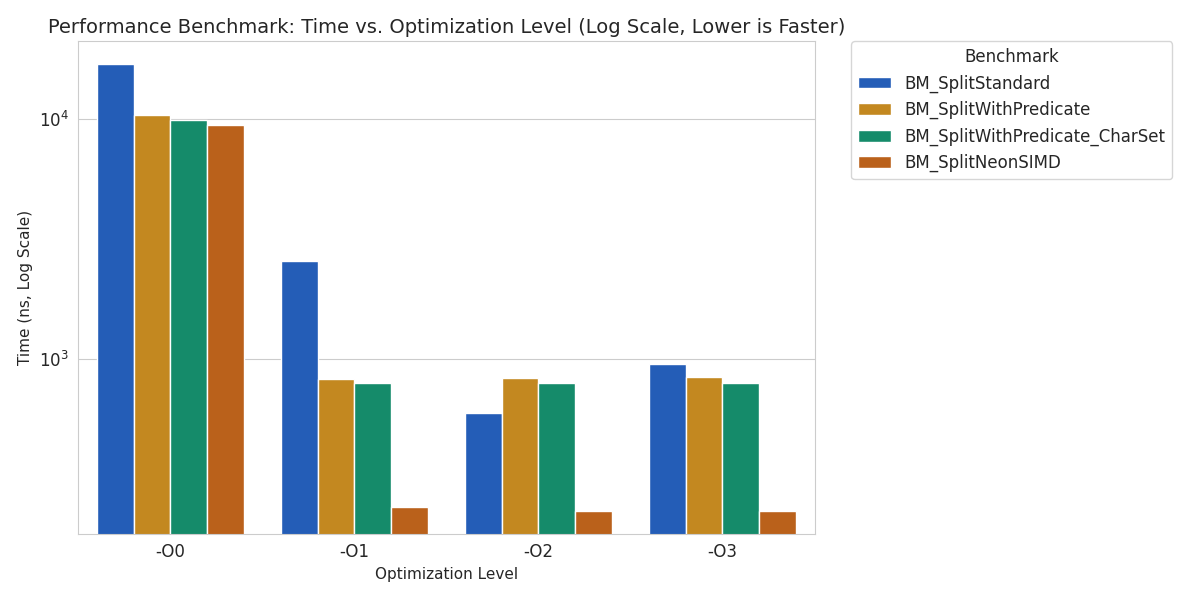
최적화 결과가 매우 좋아서 Y 축은 log scale 로 표시했습니다.

-O0 에서는 모두 고만고만 하지만, Solution 2 와 3의 경우 최적화 레벨 1~3 에서 큰 차이가 없었던 반면 SIMD 구현은 -O1 에서도 좋은 성능을 보여주었습니다.

결과적으로 -O1 에서 solution 1 의 방식을 10배 이상 빠르게 만들 수 있었습니다.

마치며

항상 그렇진 않겠지만 최적화 수준과 가독성은 trade-off 관계에 있는 것 같습니다.

주석을 달아야 이해할 수 있는 코드를 그렇게 좋아하지는 않지만 어쩔 수 없는 경우도 있는 것 같네요.

현업에서 이런 최적화 테크닉을 적용할 때는, 여러가지를 고려해야겠습니다.